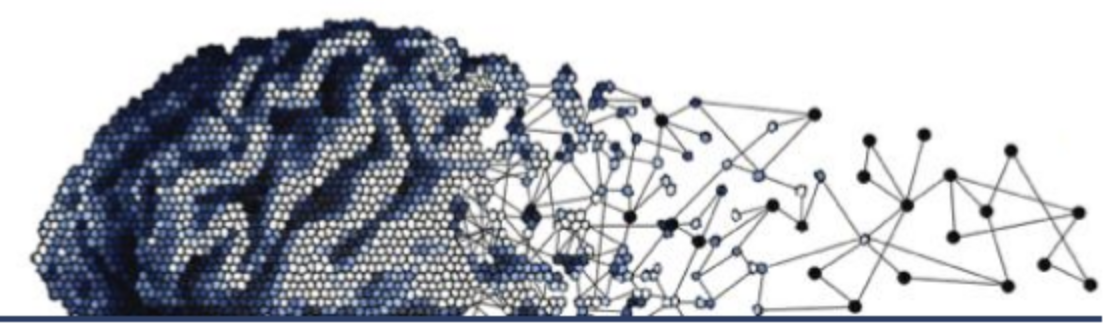
Modeling is what I do. For over a decade now people have paid me to create abstract representations of the world in order to synthesize, simulate, describe, organize, explain and most of all predict. The process by which one abstractly represents the world is called ‘modeling’ – this term aptly extends beyond computer science to the simple act of ideation. Whenever you think you create a model.
Epistemology is the branch of philosophy dedicated to understanding knowledge. It addresses questions like ‘What does it mean to know something’ and ‘Are there limits to knowledge’? I don’t pretend to be an expert in epistemology, but I find the concept very useful in the context of modeling and prediction. When I’m modeling something how do I know when to stop? What would would finding or describing a theoretical limit to my ability to model a system really mean? If epistemology is concerned with the limits of knowledge, I’m interested in the epistemology of prediction – what are the limits of prediction?
The act of mathematically modeling something is, at its core, the repeated application of mathematical transformations to arrive at better and better descriptions of the thing. I use the word ‘better’ here with intention – it’s intentionally vague. Typically better means ‘more predictive’ but it could also mean ‘faster with equal accuracy’ or even ‘more accurate with respect to component x/y/z measure, irrespective of other measures’. The raw data is itself one such description – it’s just usually not a very useful description. The task of the modeler is to extract out the predictive juices of that raw data.
The transformations we employ in this process are generally either theoretically sensible (i.e. error reduction, simple arithmetic) or have been proven in practice on similar problems or data sets (i.e. machine learning techniques, anything stochastic, encoded intuition). This transformation process can be highly complex and detailed. The limit of complexity is a model which encompasses every aspect of its subject. Put another way – the most complex and accurate model is reality itself. Predicting via abstraction (i.e. modeling) is always process of short-cutting reality. We can’t wait for reality to play out and show us what will happen, because by then it’s too late to act. What we’d like to do is ‘look ahead’ in time, to capture the crux of the process and jettison the computationally heavy and useless ‘extra stuff’ that runs orthogonal to whatever result we are concerned with.
Usually one measures progress in the modeling process by the yardstick of prediction error against some backtest. For ongoing or dynamic systems there is generally monitoring and retraining required to keep the model up to date – this retraining should happen with a frequency proportional to how likely the true nature of the system being modeled is to change through time. And, central to this thread, at no point in time is it at all clear when one should decide to stop abstracting. It’s never entirely clear when a model is finished. There’s no prescription for diagnosing when, exactly, you’ve captured every relevant bit of information of a system in your model.
This begs the question – how can we know when we’ve hit the limits of what mathematical abstraction can tell us about a given system?
Take, for a paradigmatic example, the flip of a coin. Let’s assume we want to model the outcome of this system, we want to predict the result of the next coin flip or series of coin flips. How should we proceed? Say we have a long history of flips of this particular coin. We have statistical data showing that the length of the sequence of consecutive heads or tails flipped is normally distributed around 1. In the last 1,000 tosses there have been 510 heads tossed and the last 10 tosses have been all heads.
Notice that by the very presence of numerical data we are tempted to find patterns. Our brains are masters at constructing knowledge from nothingness – a quality I think probability theorists unfairly mock. Many might presume that since 510 heads have been tossed in the last 1,000, and 10 of the last 10 tosses were heads, the best prediction for the next toss is obviously heads.
And, of course, a proper academic would scoff at this reasoning. Anyone who has read any of the pop-literature on probability theory, is familiar with the common fallacies of statistics, or has read an investment brochure will know – past results are no guarantee of future performance. But academics don’t build models in the real world. In the real world data is sparse and decisions have to be made. In fact, I think it’s difficult to construct a sensible model from the available data that would recommend anything other than heads in this situation. Yes, it’s fallacious reasoning if we assume the Platonic form of a theoretically fair coin. In the real, messy world no such coins exist. There is a good evolutionary reason that the brain is greedy (rather than conservative) pattern finding machine. Real brains jockeying for fitness in the Darwinian landscape don’t have the luxury of infinite datasets or absconding from the responsibility of decision making. Truth be told – if I absolutely had to choose given this data – I’d choose heads as well. I’d choose heads with full knowledge that, at least in the case of a theoretically perfect coin, the probability of heads is actually 50/50.
Of course, it’s important to recognize that due to limited data and our suspicions about the randomness of the underlying mechanism generating it, the nod towards heads above is as miles away from qualifying as “knowledge” about what will happen. I’d never bet money on heads with any confidence. We should not expect such naive reasoning to be particularly useful or predictive. As modelers, heads in this case is only getting our weakest possible endorsement – the ‘gun to my head’ prediction. The limits of our knowledge of this system are such that the most accurate model tells us that the outcome cannot be predicted. So, what is it about this system that makes it less predictable than other systems? Can this inform us about which other real-world systems may or may not be susceptible to predictive modeling?
To get at these questions I want to re-imagine our coin-tossing example, only this time we are demigods (already way more fun, no?). For the next toss we know all the pre-toss electrical impulses and neurochemistry going on in the tosser’s brain. We have perfect knowledge of what those signals imply about the force she is about to apply to the coin. We know the precise latitude and longitude of the locust of that force from her fingertip on the coin’s surface and can therefore calculate the velocity and rotational momentum the flip will impart. We know the humidity and air-drag on the coin’s motion, the initial height from the landing surface when tossed, the rebounding elasticity of that surface, etc. We can stop time before the flip and construct an elaborate mathematical model incorporating all of this knowledge. We can apply that model to these initial conditions to create a prediction: the coin will rotate 7 times on the way up, reach a maximum height of 15.27 inches from the table, will rotate another 12 times on the way down, bounce twice generating some very nifty collisional mechanics, spin on its axis 3 times and ultimately come to rest showing tails.
In terms of the supposed ‘randomness’ this fully grok’d version of coin-flipping is the exact opposite of the archetypal random coin-flip, yet it’s still the exact same process. The difference here is that we’ve gained access to knowledge of all the elements of the real-world system that were previously unknown, and incorporated these things appropriately into our model. The tosser’s exact brain state and its relation to the toss, the humidity in the air, the properties of the surface of the table – our lack of knowledge of these things was the true source of the randomness. Randomness can in this way be recast as a measure of our ignorance about a system or process. Once the key determinants of how the coin toss will result are known a coin toss becomes wholly deterministic.
This may not be the case for all systems. It’s possible that processes exist such that knowing precisely the initial conditions and operating rules of the system, the system is still entirely unpredictable. Quantum mechanical phenomenon immediately come to mind. This is the reason physicists are still uncertain about how to properly interpret the theory of quantum mechanics. Is it the case that there is some underlying information that would explain the apparent probabilistic nature of quantum phenomenon? Experiments like Bell’s Inequality and the Quantum Eraser double-slit experiment seem to defy any attempt at “deeper” solutions… I know because I rack my brain incessantly over the foundations of quantum mechanics and, outside of clearly understanding the mystery of it all, I haven’t made an ounce of progress.
It’s absolutely possible that the type of progress I am hoping for simply isn’t possible. Perhaps the wave functions of quantum mechanics evolve through time according to the Schrödinger equation and that is literally ‘all there is’. Most popular quantum mechanical explanations including the many-worlds interpretation and pilot-wave theory dissolve the mystery of apparent randomness in one way or another, but in exchange they demand that we believe extraordinary things about the universe, things that often hold no useful predictive value or, worse, cannot be tested. From a modeler’s perspective, quantum mechanics still holds the ultimate mystery.
But for almost every macroscopic system we care about – especially systems of risk and reward like financial markets or sports betting – we should onboard the important lesson outlined above. Apparent randomness, or the inability to predict, is a byproduct of ignorance The less we know, the more random the world appears