The SARS 2 COV outbreak has made all of us amateur epidemiologists, and I’m no exception. While epidemiology is not on my resume – I do have a lot of experience modeling and predicting complex systems. I build player-level models for sports betting, for instance, and I’ve done some work in agent-based models for disease progression using ICD9 codes, social choice theory and resource distribution, etc. Whenever possible I want to build simulations to predict things – partly because it’s really cool. More important – simulating something complex using low-level rules can reveal truths and behaviors that are obscured by top-down mathematical descriptions of a process.
We are all painfully aware of R0 – the basic reproductive number for a virus. R0 is a very useful single value measure of the infectious potential of a virus. One of my college professors had an anecdote from when he met the legendary Richard Feynman at a physics conference. Feynman – in his style – beautifully explained the inherent tradeoff between simplicity and accuracy or truth. R0 is no exception to this rule. Underlying the basic reproductive number is the complex interaction between a virus and humanity. Virus fatality rates, healthcare response, demographics, geography, connectivity, weather and – critically important for our current crisis – behavioral changes such as social distancing and impulsive hand washing all combine to define R0.
By modeling disease spread at the lowest possible granularity we can tease these various contributors to R0 apart and start to better understand, predict and prepare for future outbreaks.
As a start I’ve build a basic graph network model that evolves through time (“steps” which could represent any time increment, but for these examples can loosely be thought of as “days”). Starting from a single infected agent, agents interact randomly each day with a set probability of spreading the virus from an infected to uninfected agent on any given interaction. In every simulation the virus has an assumed fatality and recovery probability per infected person per step. It’s also assumed that recovered persons are immune to reinfection… and the dead do not reanimate 😉
Still very much a work in progress, I thought the interim results were starting to be interesting and might be worth sharing. Below are 3 different simulated scenarios.
An example agent based model of high fatality pathogen progressing through a population of 200 practicing loose social distancing (3 interactions per step/day):
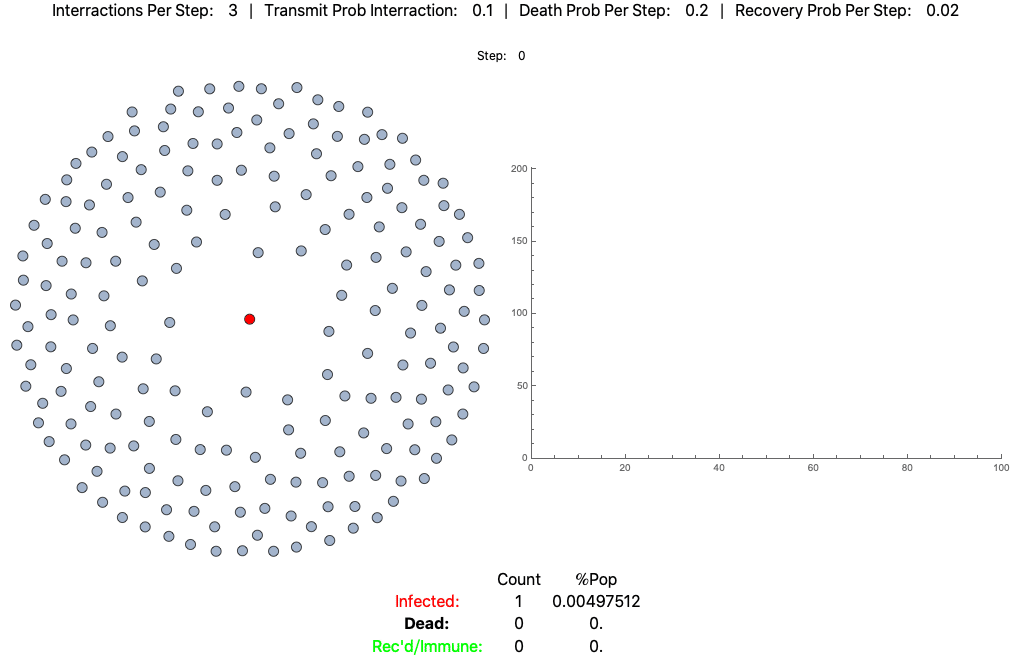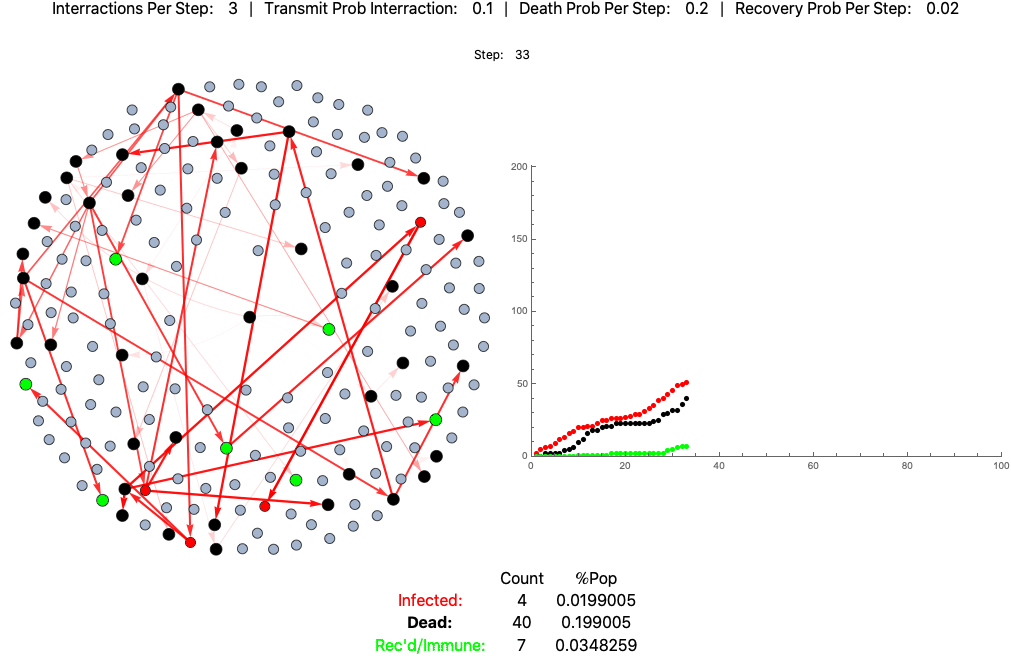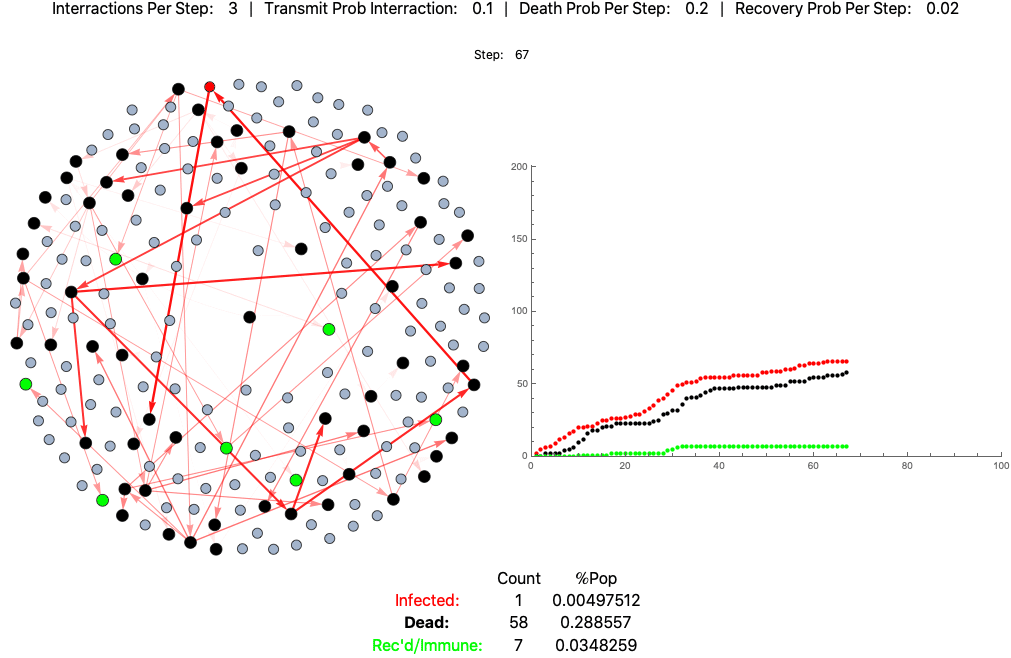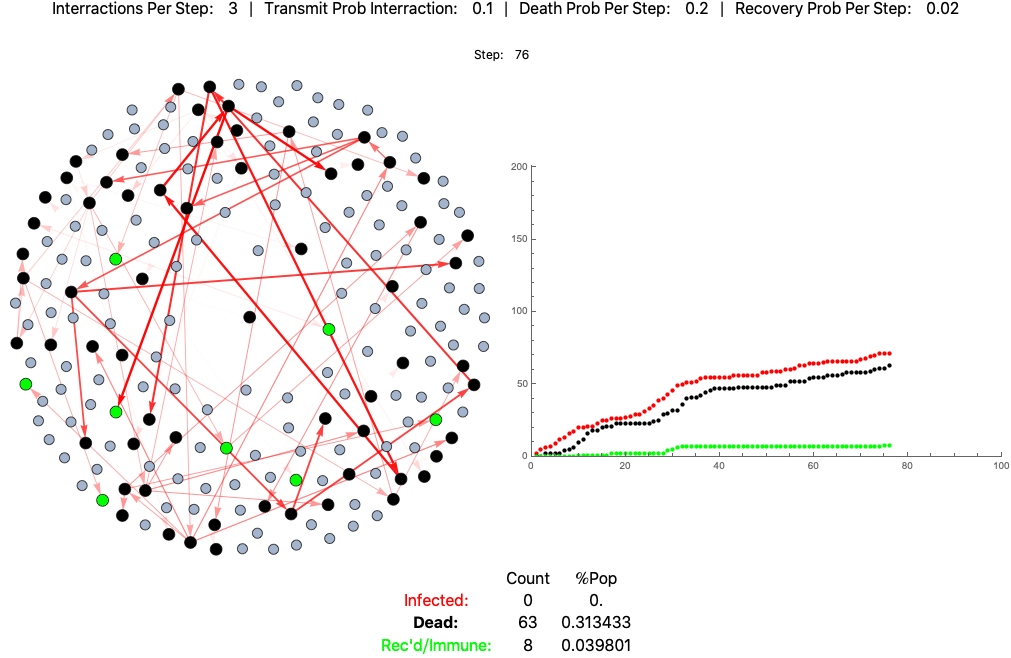
This is the same pathogen without social distancing (10 interactions per day):
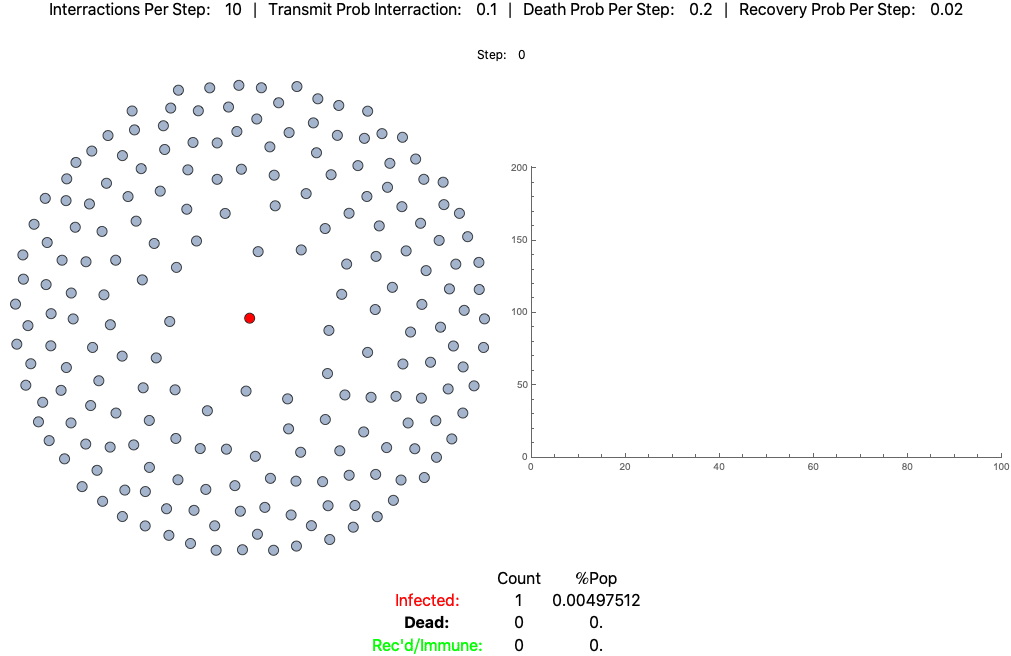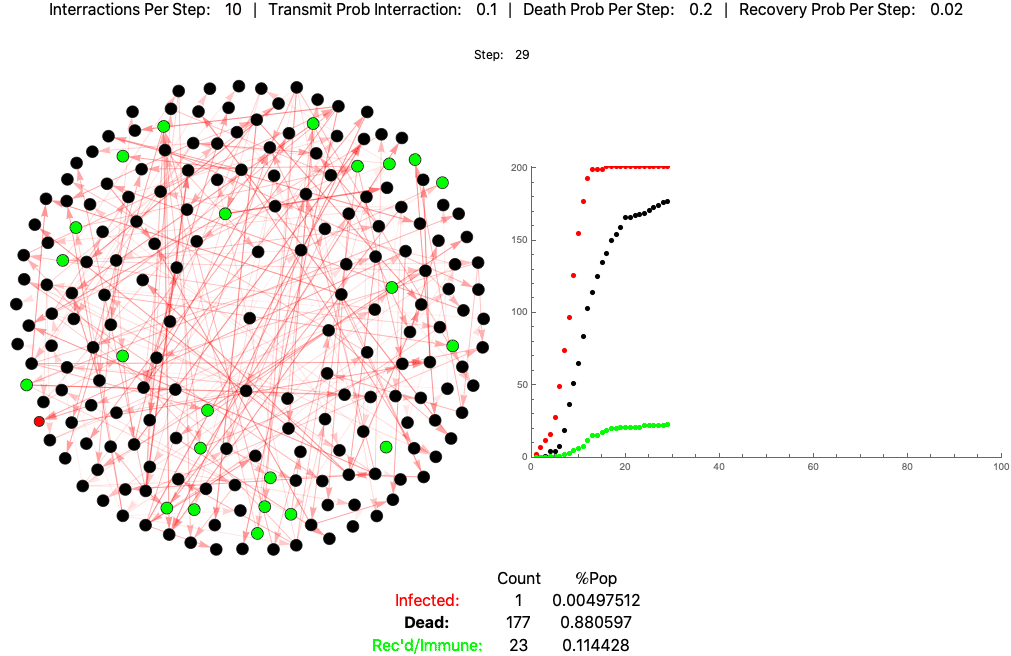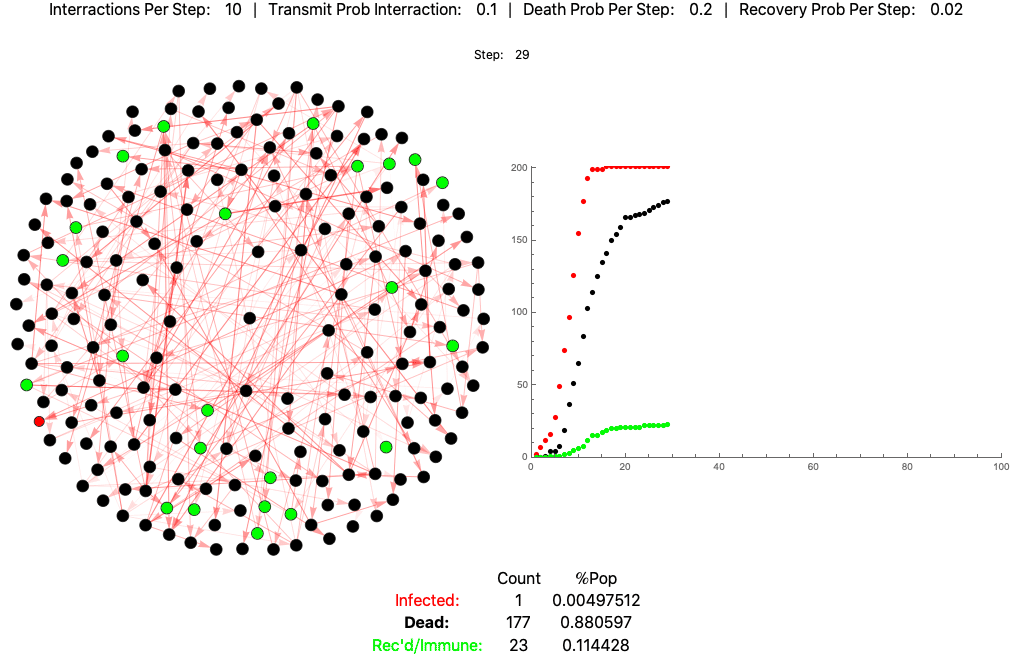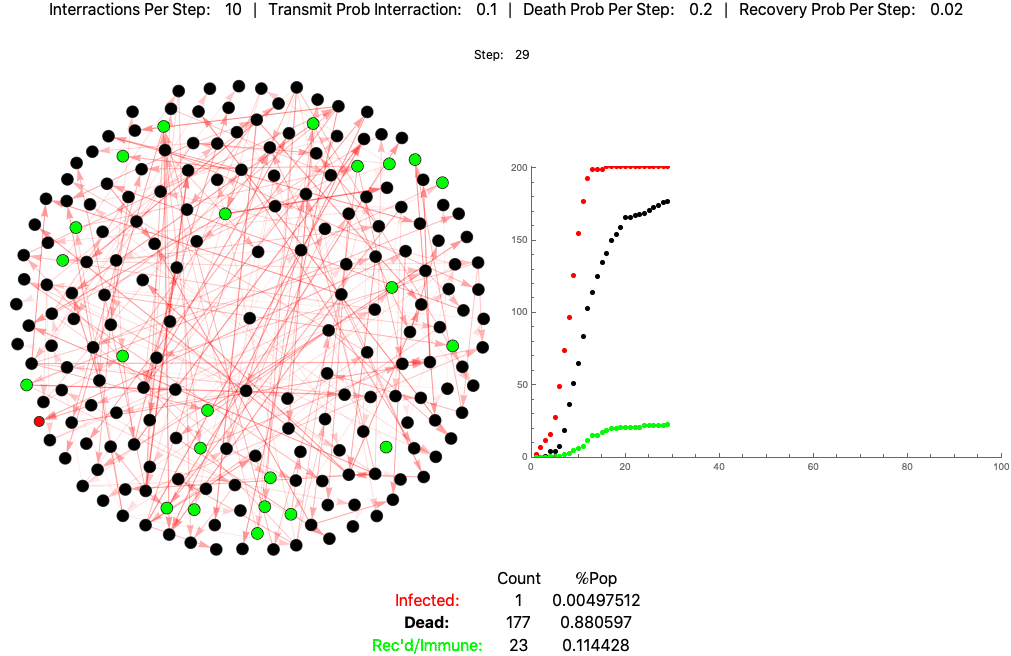
The below settings result in death rates matching the Italian scenario:
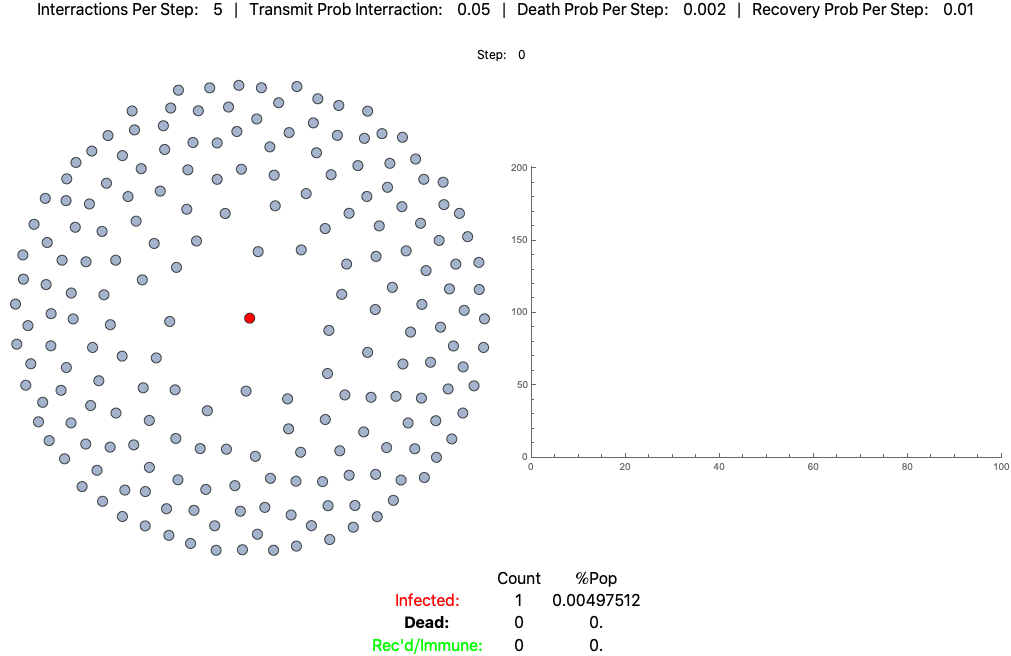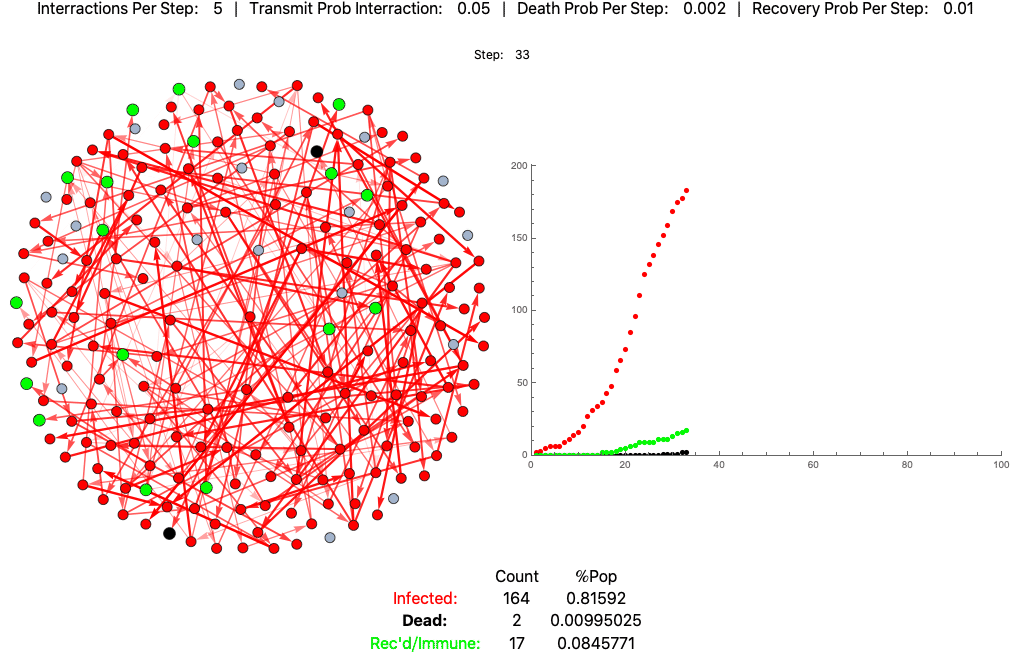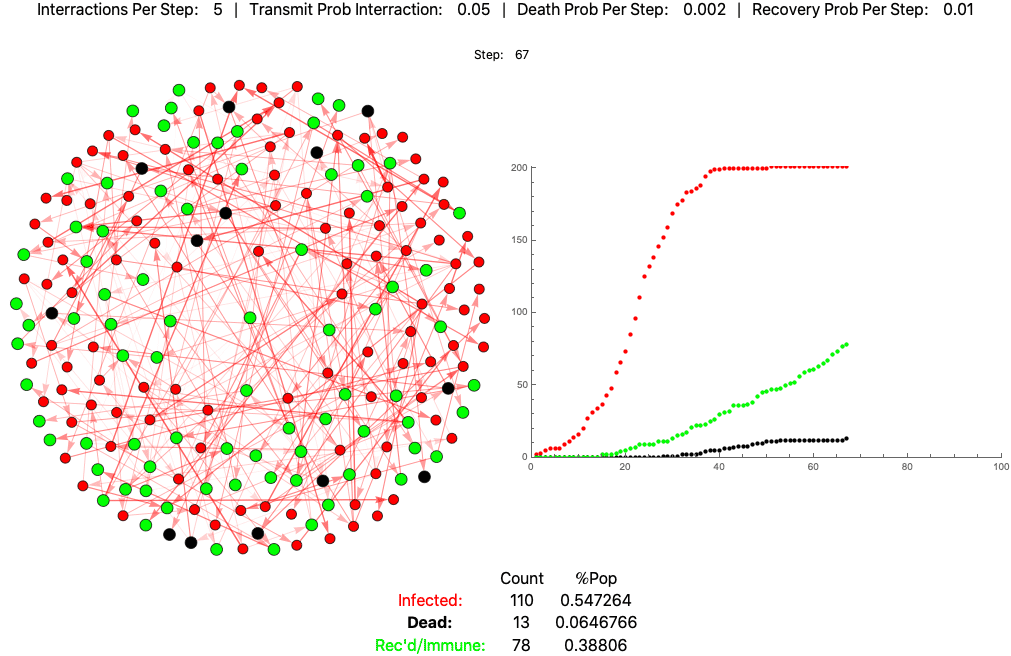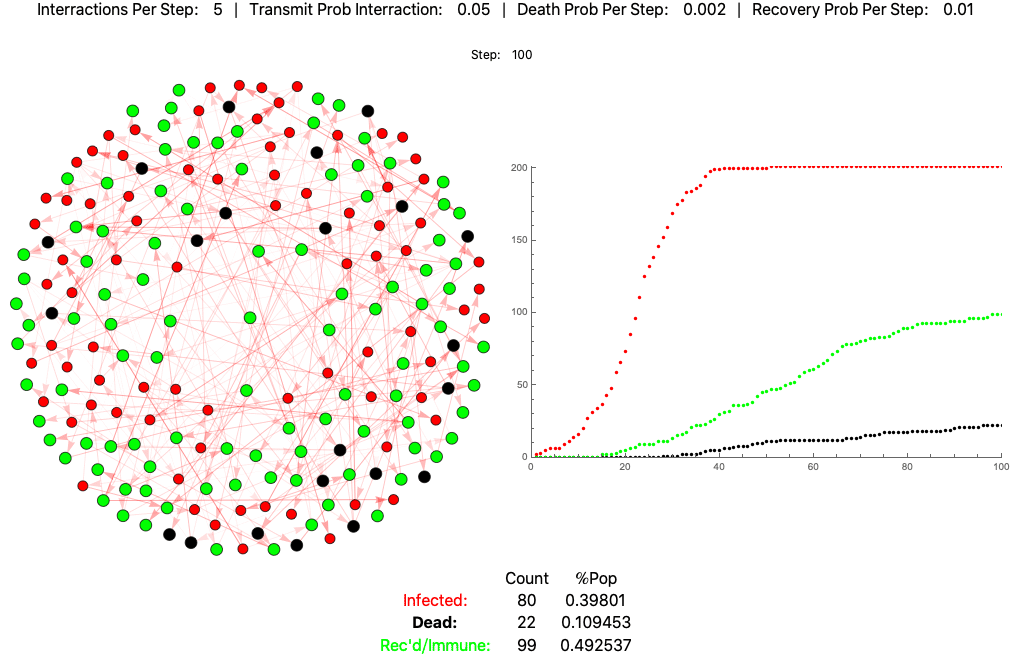
There may be lessons to extract from this approach as it is. My enthusiasm for the approach really centers on the combination of this network approach with real-world data around connectivity, geography, demographics and features of the virus. Agents can be geographically located, instead of having random interaction probabilities the probabilities can be inversely determined by distance (a proxy for connectivity). Agents can be given properties (age, gender, underlying conditions) that determine fatality rates and interaction parameters. Additional states / probabilities can be included to make more realistic simulations and measure other important outcomes like hospitalization and ICU / ventilator need.
By digging into the underlying contributors to R0 using these agent based methods we should be able to develop methods and models that help us better prepare and respond to the next big outbreak.